BioHackersNet|
Size: 1224
Comment:
|
Size: 1213
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 8: | Line 8: |
| $$ | A | = a_{i,1} * (-1)^{i+1} * M_{i,1} + a_{i,2} * (-1)^{i+2} * M_{i,2} + . . . . + a_{i,n} * (-1)^{i+n} * M_{i,n} $$ }}} |
$$ |A| = a_{i,1} * (-1)^{i+1} * M_{i,1} + a_{i,2} * (-1)^{i+2} * M_{i,2} + ... + a_{i,n} * (-1)^{i+n} * M_{i,n} $$ }}} |
| Line 11: | Line 11: |
| 이 성립한다. 이때, M_{i,j}는 A에서 i번째 행과 j번째 열을 제외한 나머지 요소들을 가지고 생성한 (n-1) * (n-1) matrix 인 cofactor A_{i,j}의 [Determinant]로, 한 수치 작아진 매트릭스를 다루게 된다. (a_{i,j} 는 A 의 (i,j) 원소를 뜻함) | 이 성립한다. 이때, M_{i,j}는 A에서 i번째 행과 j번째 열을 제외한 나머지 요소들을 가지고 생성한 (n-1) * (n-1) matrix 인 cofactor A_{i,j}의 [Determinant]로, 한 수치 작아진 [Matrix]를 다루게 된다. (a_{i,j} 는 A 의 (i,j) 원소를 뜻함) |
n*n 정방행렬의 [Determinant]를 구하기 위한 방식 중의 하나. LaplaceExpansion이라고도 한다.
대략 정리하면 다음과 같다.
A 라고 하는 n*n matrix 에서의 특정 행 혹은 열을 잡는다. i번째 행을 잡았다고 가정하였을 때,
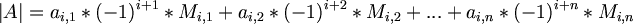
이 성립한다. 이때, M_{i,j}는 A에서 i번째 행과 j번째 열을 제외한 나머지 요소들을 가지고 생성한 (n-1) * (n-1) matrix 인 cofactor A_{i,j}의 [Determinant]로, 한 수치 작아진 [Matrix]를 다루게 된다. (a_{i,j} 는 A 의 (i,j) 원소를 뜻함)
이와 같은 과정을 거쳐서 4x4 형태의 matrix에 대한 Determinant를 구하기 위해 4개의 3x3 형태의 cofactor들의 [Determinant]를 구하게 되고, 이 3x3 matrix 형태의 [Determinant]를 구하기 위해서는 3개의 2x2 matrix 들의 [Determinant]를 구해야 한다.
이처럼 [Recursion]을 통해 계산이 가능한 2x2 matrix로의 회귀를 수행하는 것이다.
See : http://femur.wpi.edu/Learning-Modules/Linear-Algebra/solving/determinant/cofactor_expansion.html