Diff for "ConstantE" - BioHackersNet

Differences between revisions 3 and 4

constant e 무리수 2.71828....

http://mathworld.wolfram.com/e.html

$e = \lim_{n \to \infty} \left( 1 + \frac{1}{n} \right) ^n$

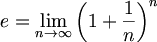
오일러의 수(Euler's number)라 불리우는 e는 스코틀란드의 에딘버그 근처에 있는 머치스톤의 영주인 네이피어(John Napier, 1550-1617))가 1614년에 발견한 것으로 곱셈을 덧셈으로 변환시킴으로 천문학적 수를 계산하는 부담을 엄첨나게 줄어 주었다. 이후 LeonhardEuler에 의해 위의 계산 식이 발견되었다.

원금이 P원이고 일년에 n번 복리로 부리될 때 t년 후의 원금의 합계 S는 S=P(1+r/n)nt 가 되는데 이 값은 일년에 아무리 많은 횟수로 복리 계산을 하더라도 무한히 늘어나지 않고 어떤 수로 수렴된다.

EulerNumber와는 다르다.

-  ⇤ ← Revision 3 as of 2005-09-07 08:20:47 → 
  Size: 1482
  Editor: 61
  Comment:
+   ← Revision 4 as of 2005-09-07 08:28:39 → ⇥
  Size: 838
  Editor: 211
  Comment: spam deleted
-Deletions are marked like this.
+Additions are marked like this.
 Line 14:
- == this is my text ==

[http://webcam.the-best.etowns.org/index.htm | web cams]
[http://webcam.the-best.etowns.org/webcam/ | webcam]
[http://webcam.the-best.etowns.org/webcams/ | webcams]
[http://webcam.the-best.etowns.org/web-cam/ | web cam]
[http://webcam.the-best.etowns.org/free-web-cams/ | free web cams]
[http://webcam.the-best.etowns.org/live-web-cams/ | live web cams]
[http://webcam.the-best.etowns.org/free-webcams/ | free webcams]
[http://webcam.the-best.etowns.org/free-webcam/ | free webcam]
[http://webcam.the-best.etowns.org/live-webcams/ | live webcams]
[http://webcam.the-best.etowns.org/live-sex/ | live sex]