일반적으로, Parameter θ와 data set D로 주어진 Model에서, θ를 위한 ML estimate는 P(D|θ)를 최대로 하는 θ이다.

likelihood에 대한 개념적 설명

주어진 모델에서 parameter(모수)가 p일 때 사건 X가 나타날 [Probability](확률)을 다음과 같이 나타낼 수 있다.

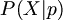
이때 주어진 데이터 X에서 parameter(모수)의 likelihood를 다음과 같이 나타낼 수 있다.

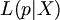
다시 말하면 [Probability](확률)는 알려진 parameter(모수)에서 결과가 나타나는 것을 예측하는 것이며 likelihood는 알려진 data에서 parameter(모수)를 측정하는 것과 관련이 있다. 따라서 MaximumLikelihood estimation은 주어진 data가 나타날 수 있는 가장 그럴듯한 확률을 구하는 것이다.

예를 들어 동전던지기를 100번 해서 앞면이 56번, 뒷면이 44번 나왔다고 했을때 MLE로 확률을 구해보자. 앞면이 나올 확률을 각각 0.5, 0.52...라고 가정하여 앞면이 56번 나올 확률을 구하면

BR

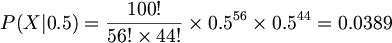
표를 만들면 다음과 같다.

p       P(X|p)
--------------
0.48    0.0222
0.50    0.0389
0.52    0.0581
0.54    0.0739
0.56    0.0801
0.58    0.0738
0.60    0.0576
0.62    0.0378

그래프를 그리면 종모양의 그림이 나온다.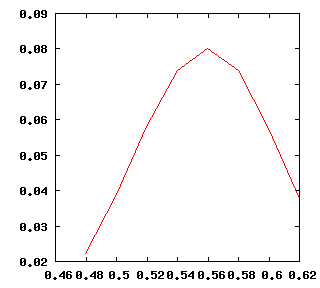

여기에서 P(X|p)를 가장 최대인 p는 0.56 이다. 따라서 주어진 data에서 MLE를 사용하여 얻은 p 값은 0.56이 된다.

주어진 예는 매우 단순하기 때문에 사실 주어진 데이터에서 0.56이 나오는 것은 당연할 결과라고 할 수 있다(=56/100). 하지만 복잡한(parameter의 수가 많은 경우와 같은)문제에서는 MLE이 유용한 도구로 사용되고 있다.

SeeAlso http://statgen.iop.kcl.ac.uk/bgim/mle/sslike_3.html

BiologicalSequenceAnalysis를 예를 들면

SwissProt내에 있는 모든 ["Protein"] 서열에 대해서 각각의 AminoAcid가 출현할 빈도, 즉 ["Probability"]를 구할 수 있다. 이러한 방법으로 20개의 AminoAcid에 대해서 각각의 빈도를 reasonable하게 이끌어 낼 수 있다. 이런 방법으로 근사하는 Model을 MaximumLikelihood estimation (ML)이라고 한다.

그외 중요한 사항들

• data set이 충분히 클 경우, ML estimation은 의미가 있으며, 작을 경우 BayesianEstimation이 사용될 수 있다.

• missing data에 대한 ML estimation 하는 일반적인 algorithm이 ExpectationMaximisation(EM) algorithm 이다.

참고사이트

• http://mathworld.wolfram.com/MaximumLikelihood.html

MaximumLikelihood 분석 프로그램

• [http://paup.csit.fsu.edu/ PAUP]