Diff for "MutualInformation"

Differences between revisions 4 and 6 (spanning 2 versions)

상호정보량. InformationTheory에서 개별 정보량과 구분되는것.

MutualInformation is the communication rate in the presence of noise.

ai와 bi의 결합확률로 평균한 것을 입력알파벳 A와 출력알파벳 B의 MutualInformation이라고 부르고, I(A;B)라고 쓴다.

$I(A;B) = H(A)-H(A|B) = \sum_{i=1}^r \sum_{j=1}^s P(a_i, b_j) \log_2 \frac{P(a_i, b_j)}{P(a_i)P(b_j)}$

$$ I(A;B) = H(B)-H(B|A) = H(A) + H(B) - H(A,B) $$

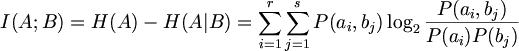
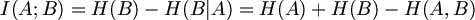
상호정보량의 의미는 B를 앎으로써, A를 표현하는 데 필요한 비트수가 몇 비트 절약될 수 있는가를 나타내고 있다. 일반적으로 A와 B에 공통으로 포함된 정보량이라고 표현할 수 있다.

-  ⇤ ← Revision 4 as of 2005-06-22 17:28:31 → 
  Size: 745
  Editor: 203
  Comment:
+   ← Revision 6 as of 2011-08-03 11:00:49 → ⇥
  Size: 751
  Editor: localhost
  Comment: converted to 1.6 markup
-Deletions are marked like this.
+Additions are marked like this.
 Line 8:
-I(A;B) = H(A)-H(A|B) = \sum_{i=1}^r \sum_{j=1}^s P(a_i, b_j) \log_2 \frac{P(a_i, b_j)}{P(a_i)P(b_j)}
+$$ I(A;B) = H(A)-H(A|B) = \sum_{i=1}^r \sum_{j=1}^s P(a_i, b_j) \log_2 \frac{P(a_i, b_j)}{P(a_i)P(b_j)} $$
 Line 10:
-[[BR]]
+<<BR>>
-Line 14:
+Line 12:
-I(A;B) = H(B)-H(B|A) = H(A) + H(B) - H(A,B)
+$$ I(A;B) = H(B)-H(B|A) = H(A) + H(B) - H(A,B) $$