|
Size: 1753
Comment:
|
← Revision 6 as of 2011-08-21 16:48:13 ⇥
Size: 1787
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| 재귀용법. ComputerScience에서 각종 [Algorithm]등에 유용하게 활용되는 기법으로, 자기자신을 호출하도록 설계하는 방법. | 재귀용법. ComputerScience에서 각종 [[Algorithm]]등에 유용하게 활용되는 기법으로, 자기자신을 호출하도록 설계하는 방법. |
| Line 10: | Line 10: |
| [Cee]의 경우 내부적으로 [Stack]을 생성한다. [Stack]의 후입선출특성이 함수의 호출종료순서와 잘 맞는다. 그러나, [Recursion]이 많은 프로그램의 경우 관련정보를 계속 유지해야하므로 많은 메모리를 사용한다. 일반적인 [Stack]레코드는 크기가 크기때문에 더욱 시간이 많이 걸린다. 어떤경우에는 이런 부담을 피하기 위해 TailRecursion이라는 특별한 형태를 사용할 수 있다. | [[Cee]]의 경우 내부적으로 [[Stack]]을 생성한다. [[Stack]]의 후입선출특성이 함수의 호출종료순서와 잘 맞는다. 그러나, [[Recursion]]이 많은 프로그램의 경우 관련정보를 계속 유지해야하므로 많은 메모리를 사용한다. 일반적인 [[Stack]]레코드는 크기가 크기때문에 더욱 시간이 많이 걸린다. 어떤경우에는 이런 부담을 피하기 위해 TailRecursion이라는 특별한 형태를 사용할 수 있다. |
| Line 19: | Line 19: |
| * [Python] code : [Factorial.py] * [Java] code : [Factorial.java] * [Cee] code : [Factorial.c] (TailRecursion 포함) * [Lisp] code : [Factorial.lisp] * [Ruby] code : [Factorial.rb] |
* [[Python]] code : [[Factorial.py]] * [[Java]] code : [[Factorial.java]] * [[Cee]] code : [[Factorial.c]] (TailRecursion 포함) * [[Lisp]] code : [[Factorial.lisp]] * [[Ruby]] code : [[Factorial.rb]] |
| Line 27: | Line 27: |
| 그외의 사용된 [Algorithm]들. | 그외의 사용된 [[Algorithm]]들. |
재귀용법. ComputerScience에서 각종 Algorithm등에 유용하게 활용되는 기법으로, 자기자신을 호출하도록 설계하는 방법.
문제를 자신보다 점점 더 작은 인스턴스들로 정의할 수 있게 하는 강력한 원리
다음의 단계를 거친다.
- 감기단계(winding) : 계속적으로 자신을 호출
- 종료조건도달
- 풀기단계(unwinding) : 최초의 호출이 리턴될때까지
Cee의 경우 내부적으로 Stack을 생성한다. Stack의 후입선출특성이 함수의 호출종료순서와 잘 맞는다. 그러나, Recursion이 많은 프로그램의 경우 관련정보를 계속 유지해야하므로 많은 메모리를 사용한다. 일반적인 Stack레코드는 크기가 크기때문에 더욱 시간이 많이 걸린다. 어떤경우에는 이런 부담을 피하기 위해 TailRecursion이라는 특별한 형태를 사용할 수 있다.
가장 흔한 예로 factorial계산 방법이 있다. (실수부분에서의 factorial계산은 StirlingFormula참고)
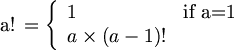
예제 코드
Python code : Factorial.py
Java code : Factorial.java
Cee code : Factorial.c (TailRecursion 포함)
Lisp code : Factorial.lisp
Ruby code : Factorial.rb
위 계산방법은 신기하게도 잘돌아가고, 성능도 좋다. 잘못쓰면 무한루프에 빠진다. 적절히 끝내는 포인트를 설정해야한다.
그외의 사용된 Algorithm들.
유사한 DesignPatterns
 BioHackersNet
BioHackersNet