|
Size: 414
Comment:
|
Size: 921
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| 1974년 헝가리의 한 교수로 부터 발명된 입체 퍼즐 |
|
| Line 3: | Line 5: |
| [http://blog.naver.com/sonmg/20020403936 맞추기 공식] | 3x3x3 Rubik's cube 의 [Permutation] 계산 {{{#!latex ( 8! \times 3^{8-1} ) \times \frac{( 12! \times 2^{12-1} )}{2} = 43,252,003,274,489,856,000 }}} 저렇게 많은 가짓수가 있지만, 최대 26번 미만의 움직임으로 모든 형태를 다 맞출 수 있다고. Solutions * David Singmaster in 1980 ([http://blog.naver.com/sonmg/20020403936 맞추기 공식]) * corners first * WikiPedia:SpeedCubing * Lars Petrus * WikiPedia:Optimal_solutions_for_Rubik%27s_Cube |
| Line 6: | Line 21: |
| 일단 공식대로 맞춰보긴 했다. 하지만,,, 단계단계의 그 이유를 잘 모르겠다. 다른면은 유지시키면서 원하는 위치만 바꾸는 요령이 필요함. 뭔가 이해를 하기엔 몇번 돌리다보면, 머리가 하얘진다는 거... -- 202.30.43.54 [[DateTime(2007-07-26T04:45:23Z)]] | 일단 공식대로 맞춰보긴 했다. 하지만,,, 단계단계의 그 이유를 잘 모르겠다. 다른면은 유지시키면서 원하는 위치만 바꾸는 요령이 필요함. 뭔가 이해를 하기엔 몇번 돌리다보면, 머리가 하얘진다는 거... -- -- ["yong27"] [[DateTime(2007-07-26T04:46:09Z)]] |
1974년 헝가리의 한 교수로 부터 발명된 입체 퍼즐
3x3x3 Rubik's cube 의 [Permutation] 계산
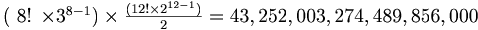
저렇게 많은 가짓수가 있지만, 최대 26번 미만의 움직임으로 모든 형태를 다 맞출 수 있다고.
Solutions
David Singmaster in 1980 ([http://blog.naver.com/sonmg/20020403936 맞추기 공식])
- corners first
- Lars Petrus
일단 공식대로 맞춰보긴 했다. 하지만,,, 단계단계의 그 이유를 잘 모르겠다. 다른면은 유지시키면서 원하는 위치만 바꾸는 요령이 필요함. 뭔가 이해를 하기엔 몇번 돌리다보면, 머리가 하얘진다는 거... -- -- ["yong27"] DateTime(2007-07-26T04:46:09Z)
 BioHackersNet
BioHackersNet