|
Size: 846
Comment: converted to 1.6 markup
|
← Revision 4 as of 2011-08-21 16:46:21 ⇥
Size: 850
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| 행렬식(Determinant) in [Matrix] | 행렬식(Determinant) in [[Matrix]] |
| Line 39: | Line 39: |
| 기본적으로 n차 정방행렬의 행렬식([Determinant])은 내포된 n-1차 정방행렬의 행렬식에 의해 귀납적으로 계산될 수 있다. (recursion) | 기본적으로 n차 정방행렬의 행렬식([[Determinant]])은 내포된 n-1차 정방행렬의 행렬식에 의해 귀납적으로 계산될 수 있다. (recursion) |
행렬식(Determinant) in Matrix
2*2 matrix
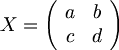
일때,
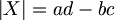
3*3 matrix
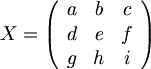
일때,
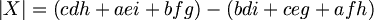
n * n matrix
n*n 정방행렬(square matrix of order n) 의 경우는 LaplaceExpansion (= CofactorExpansion)에 의해 계산되어질 수 있다.
기본적으로 n차 정방행렬의 행렬식(Determinant)은 내포된 n-1차 정방행렬의 행렬식에 의해 귀납적으로 계산될 수 있다. (recursion)
 BioHackersNet
BioHackersNet