EigenValue와 EigenVector의 정의

n*n 형태의 matrix인 P가 있다고 했을때, 특정 matrix A에 대하여 다음과 같은 식이 성립하는 실수 lambda가 있다고 하자.

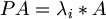
이때의 lambda를 EigenValue라고 하고, matrix A를 right EigenVector라고 한다.

경우에 따라,

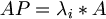
인 경우가 있는데, 이때의 matrix A를 left EigenVector라고 한다.

EigenValue와 EigenVector 구하기

여기서 EigenValue와 EigenVector는 다음과 같은 순서로 구한다.

맨 위의 식을 A에 대해 묶으면,

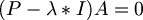
여기에서

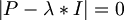
를 이용하여 lambda 값을 구한다. (어떻게? ) 참고 : | X | 는 matrix X의 [Determinant]임

구한 lambda을 (1)의 식에 대입하여 EigenVector값인 A를 구한다.

위의 경우, EigenVector는 항상 right의 경우 1*n 혹은 left의 경우 n*1의 형태인 matrix인가요?

• 보통, LinearAlgebra에서 말하는 벡터는 행하나짜리 혹은 열하나짜리 [Matrix]를 뜻함