|
Size: 2104
Comment:
|
Size: 2745
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| #acl yong27:admin | |
| Line 4: | Line 3: |
| [Recursion]으로 다음처럼 계산한다. | 본 계산은 [Recursion]을 이용한다. 짧은 서열에 대해 최적구조를 계산하고, 이를 크게 확장시켜나간다. 재귀의 키포인트는 짧은 서열에서의 최적구조 i, j는 다음의 4가지 종류만이 있다는 점이다. |
| Line 10: | Line 9: |
| delta(i,j)를 정의하고 i, j가 base pair이면 1, 아니면 0을 준다. {{{ |
길이 L의 서열 x {{{#!latex $$ x_1,...,x_L $$ }}} 에서 base pairing 이 일어나는 위치는 구하는 알고리즘은 다음의 두 단계로 이루어진다. == Fill stage == delta(i,j)를 정의하고 i, j가 complementary base pair이면 1, 아니면 0을 준다. 그리고는 점수 gamma(i,j)를 다음처럼 구한다. Initialisation {{{#!latex $$ \gamma(i, i-1) = 0 \textrm{ for } i = 2 \textrm{ to } L; $$ $$ \gamma(i, i) = 0 \textrm{ for } i = 1 \textrm{ to } L; $$ }}} |
| Line 20: | Line 31: |
| }}} | == Traceback stage == |
RnaSecondaryStructurePrediction에서 DynamicProgramming에 기반한 [RNA] 2차구조 예측 [Algorithm]. 정확한 예측은 무리. 그러나 짧은 [RNA]에 대해서는 비교적 정확한 결과를 제공한다.
본 계산은 [Recursion]을 이용한다. 짧은 서열에 대해 최적구조를 계산하고, 이를 크게 확장시켜나간다. 재귀의 키포인트는 짧은 서열에서의 최적구조 i, j는 다음의 4가지 종류만이 있다는 점이다.
- add unpaired position i onto bast structure for subsequence i+1, j
- add unpaired position j onto best structure for subsequence i, j-1
- add i, j pair onto best structure found for subsequence i+1, j-1
- combine two optimal substructures i, k and k+1, j
길이 L의 서열 x 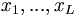
에서 base pairing 이 일어나는 위치는 구하는 알고리즘은 다음의 두 단계로 이루어진다.
Fill stage
delta(i,j)를 정의하고 i, j가 complementary base pair이면 1, 아니면 0을 준다. 그리고는 점수 gamma(i,j)를 다음처럼 구한다.
Initialisation 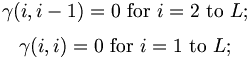
Initialisation: gamma(i, i-1) = 0 for i = 2 to L;
- gamma(i, i) = 0 for i = 1 to L.
Recursion: starting with all subsequences of length 2, to length L:
- { gamma(i+1, j),
gamma(i,j) = max { gamma(i, j-1),
- { gamma(i+1, j-1) + delta(i,j),
{ max(i<k<j, [ gamma(i,k) + gamma(k+1,j) ].
Traceback stage
trace back은 ["Stack"]을 써서 다음처럼 한다.
Initialisation: Push(l,L) onto stack.
Recursion: Repeat until stack is empty:
- pop (i,j)
- if i >= j continue;
else if gamma(i+1,j) = gamma(i,j), push (i+1, j);
else if gamma(i,j-1) = gamma(i,j), push (i, j-1);
else if gamma(i+1, j-1) + delta(i,j) = gamma(i,j):
- record i, j base pair.
- push (i+1, j-1).
else for k = i+1 to j-1: if gamma(i,k) + gamma(k+1, j) = gamma(i,j):
- push (k+1, j).
- push (i,k).
- break.["Python"]Code: [Nussinov.py], UnitTest code [TestNussinov.py]
(DeleteMe 12월 11일 현재 완료하긴 했는데 교재랑 결과값이 다르게 나옵니다. 책대로라면, 서열 GGGAAAUCC 에 대해 [(2,9),(3,8),(4,7)]가 나와야하는데 [(2,9),(3,8),(6,7)]이 출력됩니다. 책 그림을 봐도 마지막부분에 1에서 1로 가야하는데 0 으로 가버리네요)
See also ScfgNussinovAlgorithm (StochasticContextFreeGrammar-based algorithm)
 BioHackersNet
BioHackersNet