ParametricPlot - BioHackersNet

매개변수를 이용한 플랏.

http://www.physics.ohio-state.edu/~physedu/mapletutorial/tutorials/kinematics2/parametric.html

평면좌표에서 (x,y)를 (f(t), g(t))로 표현한뒤 그린다.

만일 원을 ParametricPlot으로 그린다면?

$\math{ x^2 + y^2 = 1 }$

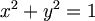
윗식은 (t, sqrt(1-t^2)) 으로 표현가능하므로, 아래처럼 그릴 수 있다.

set parametric
set xrange [-1.5:1.5]
set yrange [-1.5:1.5]
plot t, sqrt(1-t**2), t, -sqrt(1-t**2)

유명한식

$\math{ {\sin{\theta}}^2 + {\cos{\theta}}^2 = 1 }$

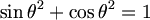
을 이용하면 곧 (sin(t), cos(t)) 이므로, 아래와도 같다.

set parametric
set xrange [-1.5:1.5]
set yrange [-1.5:1.5]
plot sin(t), cos(t)

근데 왜 GnuPlot은 두 그래프를 다르게 그리는가? (특히 y=0부근) 유추하건데, 컴퓨터의 부동소수표현과도 관련있는 NumericalAnalysis 문제인듯하다. 0에 가까운 작은 수를 제곱해서 루트를 씌운다는것 자체가 이미 많은 에러를 포함하고 있다. 0에 가까이 다가갈수록 더욱 에러는 커지고... 또 한가지 이유는, GnuPlot는 유사한 두 지점을 선으로 연결하지만, 위 첫번째그림에서는 따로따로 그려진 저 부분을 연결할 수 없기에, 저렇게 그린듯.

SeeAlso LoveEquation