PearsonCorrelation - BioHackersNet

두 변수사이의 관계가 얼마나 상호관계되어있냐를 정량화한 상수

http://davidmlane.com/hyperstat/A34739.html

$r_{xy} = \frac{ \frac{ \sum(x-\overline{x})(y-\overline{y}) }{n-1} }{ \sqrt{ \frac{\sum(x-\overline{x})^2}{n-1} } \sqrt{ \frac{\sum(y-\overline{y})^2}{n-1}} }$

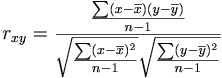
예를 들어, 어린아이의 키와 나이라는 두 변수를 고려할 때 (예로, 그냥 20세까지만이라고 하자) 이 두변수는 상호 관련이 있다. 나이가 증가할 수록 키도 같이 증가하기 때문이다. 또한, 어느 한 시기의 술소비량증가과 교통사고 증가율 같은 경우, 미미하지만 둘 사이는 관련이 있다.

이렇게 상호 관계가 있는 두 변수가 얼마나 관련되어있느냐를 정량화한 상수로서 정확히 1:1관계, y=x를 이루고 있으면 PearsonCorrelation 은 +1값을 가지며, 관계가 적어질 수록 1 밑으로 떨어지고, 전혀 상관관계가 없을 경우 0이 된다. 또한 역관계에 있을 경우는 (y=-x) -1로 표기된다.

따라서 -1 < PearsonCorrelation < 1 의 관계를 가진다.