가장 중요한 CountingProcess 의 하나.
정의: The CountingProcess {N(t), t>=0} is said to be a PoissonProcess having rate $$ \lambda, \lambda > 0 $$, if
(i) N(0)= 0 (ii) The process has independent increments. (iii) The number of events in any internal of length t is Poisson distributed with mean t. That is, for all s, t>=0
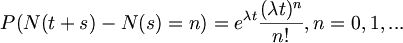
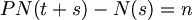
 BioHackersNet
BioHackersNet