귀류법. Reduction to the absurd (모순).

어떤 명제가 참임을 증명하기 위해 그 명제의 역이 참이라고 일단 가정한 뒤, 이 역명제가 성립할 때 초래될 수밖에 없는 모순을 지적함으로써 원래 명제가 참임을 간접적으로 밝히는 논증법.

2의 제곱근은 무리수이다 라는 명제를 귀류법으로 증명하면,

2의 제곱근은 유리수이다 라고 가정한다면, 유리수이므로 두개의 정수비로 나타낼 수 있어야 한다.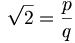

p와 q의 크기는 제한이 필요없지만, 공약수가 없어야 한다. 만일 있다면 약분하여, 더이상 약분할 수 없을 때의 값을 p,q라고 하면 된다. 양변을 제곱하면,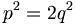

여기에서, p는 짝수임을 알 수 있다. 따라서 p를 또하나의 정수 2s라고 쓴다면,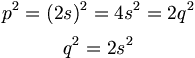

q역시 짝수여야 한다. 그렇다면 위의 과정에서 2로도 약분될 수 있다는 이야기이므로, 가정이 틀리다는 이야기이며, 이로서, 제곱근 2가 무리수임이 증명된다.