함수 f(t)를 s에 대한 함수로 변환한 식.
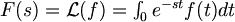
을 함수 f(t)의 라플라스변환이라고 한다. PierreSimonLaplace에 의해 정리됨
보통, DifferentialEquation을 풀기 위해서 활용되는데, 이유는 선형상미분방정식을 대수방정식으로 변환할 수 있기 때문이다.
Laplace 변환의 기본개념은 주어진 어려운 문제를 쉬운 문제로 변환 시켜 대수적인 방법을로 풀고 다시 역변환에 의해 주어진 문제의 해를 구하는 것이다. 미분 방정식에서의 이 변환은 대단히 효율적이며 실제 응용에 중요한 가치를 가지고 있다.
임의의 계의 지배방정식이 선형 상미분 방정식으로 표현될 경우, LaplaceTransform을 통하여 계의 특성을 해석하기도 한다.
FourierTransform과는 달리 적분의 형태가 0에서 무한대에 걸쳐 있으며, 따라서 초기조건에 대한 고려가 자연스럽게 가능한 형태를 갖고 있다. 소음진동의 경우 이 변환방법을 통하여 해석적인 해를 얻는 방법을 많이 사용하고 있다. s중 실수부의 부호는 해의 발산, 수렴 즉 응답의 안정성등을 이해하는 척도로 사용되며, 허수부는 주파수로 이해하여 사용한다.
관련수식
1. Definition :
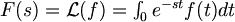
2. Linearity :
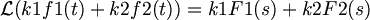
3. Time Shift :
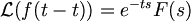
6. Differentiation :
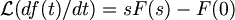
 BioHackersNet
BioHackersNet