Differences between revisions 2 and 3
⇤ ← Revision 2 as of 2005-08-17 11:26:48 →
Size: 4556
Editor: 203
Comment: fix latex format
← Revision 3 as of 2011-08-03 11:00:44 → ⇥
Size: 4556
Editor: localhost
Comment: converted to 1.6 markup
Deletions are marked like this. Additions are marked like this.
Line 33: Line 33:
whici are the ["Probability"] of the substitution of b by a occurring via some intermediate, c. whici are the [[Probability]] of the substitution of b by a occurring via some intermediate, c.

PercentAcceptedMutation. One of the SubstitutionMatrix.

MargaretDayhoff, Schwartz & Orcutt가 1978년 만듬.

The basis of their approach is to obtain substitution data from alignments between very similar proteins, allowing for the evolutionary relationships of the proteins in families, and then extrapolate this information to longer evolutionary distances.

  1. 15%이상 다르지 않은 서열로만 71 family로 hypothetical PhylogeneticTree를 만듬.

  2. tree를 만들기 위해 ParsimonyMethod 사용

  3. Aab를 축적시킴 (Aab containing the frequencies of all pairings of residues a and b between sequences and their immediate ancestors on the tree.
  4. 진화의 방향은 무시

ConditionalProbability P(b|a,t): a is substituted by b in time t.

$$ P(b|a,t) = \frac{P_{ab}(t)}{q_a} $$

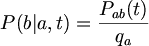
The short time interval estimates for P(b|a) can be derived from the Aab matrix by setting

$$ P(b|a) = B_{a,b} = \frac{A_{a,b}} { \sum_c A_{ac}} $$

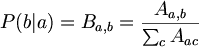
These values must next be adjusted to correct for divergence time t. residue a accurs at the frequency Qa, is SUM(Qa Qb Bab). Dayhoff defined a SubstitutionMatrix to be a 1 PAM matrix.

1 PAM matrix = expected number of substitution was 1% = SUM(Qa Qb Bab) = 0.01

For longer times, S(1) is raised to a power n, giving S(n) = S(1)^n. 

S(2), the matrix product of S(1) with itself, 
has entries P(a|b,t=2) = SUM( P(a|b,t=1) P(a|b,t=1) )

whici are the Probability of the substitution of b by a occurring via some intermediate, c.

S(n) represents the result of n steps of a MarkovChain with 20 states.

Finally, a matrix of scores is obtained from S(t). Since P(b|a) = Pab/Qa, the entries of the score matrix for time t are given by

$$ s(a,b|t) = \log \frac{P(b|a,t)}{q_b} $$

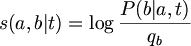
PAM30 

# This matrix was produced by "pam" Version 1.0.6 [28-Jul-93]
#
# PAM 30 substitution matrix, scale = ln(2)/2 = 0.346574
#
# Expected score = -5.06, Entropy = 2.57 bits
#
# Lowest score = -17, Highest score = 13
#
    A   R   N   D   C   Q   E   G   H   I   L   K   M   F   P   S   T   W   Y   V   B   Z   X   *
A   6  -7  -4  -3  -6  -4  -2  -2  -7  -5  -6  -7  -5  -8  -2   0  -1 -13  -8  -2  -3  -3  -3 -17
R  -7   8  -6 -10  -8  -2  -9  -9  -2  -5  -8   0  -4  -9  -4  -3  -6  -2 -10  -8  -7  -4  -6 -17
N  -4  -6   8   2 -11  -3  -2  -3   0  -5  -7  -1  -9  -9  -6   0  -2  -8  -4  -8   6  -3  -3 -17
D  -3 -10   2   8 -14  -2   2  -3  -4  -7 -12  -4 -11 -15  -8  -4  -5 -15 -11  -8   6   1  -5 -17
C  -6  -8 -11 -14  10 -14 -14  -9  -7  -6 -15 -14 -13 -13  -8  -3  -8 -15  -4  -6 -12 -14  -9 -17
Q  -4  -2  -3  -2 -14   8   1  -7   1  -8  -5  -3  -4 -13  -3  -5  -5 -13 -12  -7  -3   6  -5 -17
E  -2  -9  -2   2 -14   1   8  -4  -5  -5  -9  -4  -7 -14  -5  -4  -6 -17  -8  -6   1   6  -5 -17
G  -2  -9  -3  -3  -9  -7  -4   6  -9 -11 -10  -7  -8  -9  -6  -2  -6 -15 -14  -5  -3  -5  -5 -17
H  -7  -2   0  -4  -7   1  -5  -9   9  -9  -6  -6 -10  -6  -4  -6  -7  -7  -3  -6  -1  -1  -5 -17
I  -5  -5  -5  -7  -6  -8  -5 -11  -9   8  -1  -6  -1  -2  -8  -7  -2 -14  -6   2  -6  -6  -5 -17
L  -6  -8  -7 -12 -15  -5  -9 -10  -6  -1   7  -8   1  -3  -7  -8  -7  -6  -7  -2  -9  -7  -6 -17
K  -7   0  -1  -4 -14  -3  -4  -7  -6  -6  -8   7  -2 -14  -6  -4  -3 -12  -9  -9  -2  -4  -5 -17
M  -5  -4  -9 -11 -13  -4  -7  -8 -10  -1   1  -2  11  -4  -8  -5  -4 -13 -11  -1 -10  -5  -5 -17
F  -8  -9  -9 -15 -13 -13 -14  -9  -6  -2  -3 -14  -4   9 -10  -6  -9  -4   2  -8 -10 -13  -8 -17
P  -2  -4  -6  -8  -8  -3  -5  -6  -4  -8  -7  -6  -8 -10   8  -2  -4 -14 -13  -6  -7  -4  -5 -17
S   0  -3   0  -4  -3  -5  -4  -2  -6  -7  -8  -4  -5  -6  -2   6   0  -5  -7  -6  -1  -5  -3 -17
T  -1  -6  -2  -5  -8  -5  -6  -6  -7  -2  -7  -3  -4  -9  -4   0   7 -13  -6  -3  -3  -6  -4 -17
W -13  -2  -8 -15 -15 -13 -17 -15  -7 -14  -6 -12 -13  -4 -14  -5 -13  13  -5 -15 -10 -14 -11 -17
Y  -8 -10  -4 -11  -4 -12  -8 -14  -3  -6  -7  -9 -11   2 -13  -7  -6  -5  10  -7  -6  -9  -7 -17
V  -2  -8  -8  -8  -6  -7  -6  -5  -6   2  -2  -9  -1  -8  -6  -6  -3 -15  -7   7  -8  -6  -5 -17
B  -3  -7   6   6 -12  -3   1  -3  -1  -6  -9  -2 -10 -10  -7  -1  -3 -10  -6  -8   6   0  -5 -17
Z  -3  -4  -3   1 -14   6   6  -5  -1  -6  -7  -4  -5 -13  -4  -5  -6 -14  -9  -6   0   6  -5 -17
X  -3  -6  -3  -5  -9  -5  -5  -5  -5  -5  -6  -5  -5  -8  -5  -3  -4 -11  -7  -5  -5  -5  -5 -17
* -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17   1

PAM (last edited 2011-08-03 11:00:44 by localhost)

web biohackers.net