PairwiseAlignment의 LocalAlignment 버젼. 1981년 Smith & MichaelWaterman에 의해 소개됨. NeedlemanWunschAlgorithm이 GlobalAlignment의 방법인데 비해, 부분적 서열의 정렬을 가능케 함.

s = AGCACAGA, t = ACACACTA

두 서열이 있을 때 s와 t를 각각 행렬의 축으로 하고 unit cost model(일치=0, 치환, 삽입, 삭제=1)을 이용하여 각각의 행렬의 항들을 채워나간다.

위에서 대각선으로 최소값을 나타내는 행로를 표시하면 그 행로에 대한 점수를 매길 수 있다. 서열 s에 대하여 대각선은 일치, 혹은 치환을, 수평선은 삽일을, 수직선은 삭제를 나태낸다. 때때로 적절한 배열을 위한 최소한의 행로는 단 한개가 아니고 여러개가 될 수 있다. 대각선에 의해 표시된 행로에 의해 s와 t를 배열하면 다음과 같다.

s = AGCACAC-A
t = A-CACACTA

이와 같이 DynamicProgramming을 이용하여 임의의 서열과 데이터베이스에 저장된 서열들을 비교하는 방법을 SmithWatermanAlgorithm이라 한다. 현재 이 알고리즘을 이용하여 유사성 검색 서비스를 제공하는 곳은 EBI의 BLITZ와 Bic-sw Database Searches가 있다.

EBI에서 제공하는 Smith-Waterman 서열분석 서비스는 Bic-sw Database Searches (http://www2.ebi.ac.uk/Bic-sw) 로서 서열을 입력하면 Web 혹은 E-mail을 통하여 검색결과를 보내준다.

See also SequenceHomologySearch

linear score로 Gap penalty를 적용했을 때의 수식을 보면,

initionally

• F(0,0) = 0
• i=0 에서 F (0,j) = -d j
• j=0 에서 F (i,0) = -d i

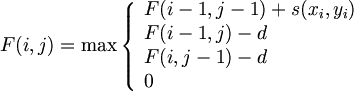
negative score에 값 0을 줌으로써 0인곳에서 새롭게 alignment를 시작할 수 있다. 이때 alignment의 끝부분은 score의 maximum값이 있는 곳. 그곳에서 traceback하여 0까지 하면 된다.

LocalAlignment가 동작하기 위해서 random match의 expected score는 negative여야 한다. 그렇지 않으면, 전체적으로 비교적 덜 상관있는 두 서열의 긴 match에 의해 높은 점수를 가질 수 있다. 따라서, 비록 알고리즘은 local이지만, maximal scoring alignments는 global이어야 한다. true sebsequence alignment는 보다 긴 incorrect alignment에 의해 가려져야 한다.

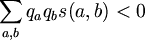
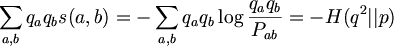
H(q^2 || P) is the RelativeEntropy of distribution q^2 = q * q with respect to distribution P, --> always positive