BiologicalSequenceAnalysis의 한 방법. Sefiroth에서 BioPythonTestDrivenDevelopment 대상 1호

Contents

  1. Introduction
  2. The scoring model
  3. Alignment algorithm
  4. DynamicProgramming with more complex model
    1. Alignment with affine gap scores
    2. More complex FSA models
  5. HeuristicAlgorithm
    1. BLAST
    2. FASTA
  6. Linear space alignment
  7. Significance of scores
    1. The Bayesian approach: model comparison
    2. The Classical approach: the extream value distribution
    3. Correcting for length
    4. Why use the alignment score as the test statistic?
  8. Deriving score parameters from alignment data
    1. Dayhoff PAM matrices and BLOSUM matrices
    2. Estimating gap penalties
  9. PairwiseAlignment using HMMs

Introduction

서열분석의 기본은 두 서열이 서로 얼마나 연관되어있을지를 보는것.

Key issue:

  1. 어떤형태의 alignment를 고려할것인가
  2. 어떤 Scoring system을 써서 alignment의 순위를 매길것인가
  3. 최적의 점수를 받는 alignment를 만들 수 있는 알고리즘
  4. alignment점수의 유의성을 계산하기 위한 통계적 방법

BLAST에서 만들어낸 PairwiseAlignment의 일부 (SubstitutionMatrix BLUSOM 62 사용) 

>sp|P19549|ENV_HV1S3 ENVELOPE POLYPROTEIN GP160 PRECURSOR [CONTAINS: EXTERIOR MEMBRANE
           GLYCOPROTEIN (GP120); TRANSMEMBRANE GLYCOPROTEIN (GP41)]
          Length = 852

 Score =  182 bits (461), Expect = 9e-46
 Identities = 117/381 (30%), Positives = 182/381 (47%), Gaps = 31/381 (8%)

Query: 4   LRYCAPAGFALLKCNDADYDGFKTNCSNVSVVHCXXXXXXXXXXXXXXXGSYSENRTQIW 63
           + YCAPAGFA+LKCN+  + G K  C+NVS V C               GS +E    I 
Sbjct: 216 IHYCAPAGFAILKCNNKKFSG-KGQCTNVSTVQCTHGIKPVVSTQLLLNGSLAEEEVVIR 274

The scoring model

  • Basic mutation (change residues) : Substitution
  • Insertion, Deletions (add or remove residus) : Gap
  • Logarithm of the relative likelihood
  • Total score = terms for each aligned pair + terms for each gap
  • assumption : mutations at different sites in a sequence to be occurred independently

odds ratio = match model likelihood / random model likelihood

LogOddsRatio s(a, b) = log(Pab / Qa Qb)

SubstitutionMatrix : s(xi, yi)

Gap penalites (g:gap length)

  • linear score
    • 벌점(g) = -gd
    • 일반적으로 d=8을 사용
  • affine score
    • 벌점(g) = -d(g-1)e
    • d : gap-open penalty (보통 12)
    • e : gap-extension penalty (보통 2)

Alignment algorithm

두 서열간에 가능한 총 GlobalAlignment 갯수 (same length n 일때)

$$ { 2n \choose n } = \frac{(2n)!}{(n!)^2} \simeq \frac{2^{2n}}{\sqrt{2 \pi n}} $$

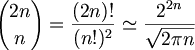
Computationally 계산 불가능. 따라서 DynamicProgramming의 방법을 쓴다.

The goal of an alignment algorithm is to incorporate as many of these positively scoring pairs as possible into the alignment, while minimising the cost from unconserved residu pairs, gaps, and other constraints.

4가지 상이한 alignment 방법들이 있다.

예제코드 : PairwiseAlignmentLinearGap.py

모든 alignment method는 다음의 조합

  • matrix F(i,j)
  • boundary conditions
  • recurrence rule 의 적용

When performing a sequence similarity search we should ideally always consider what types of match we are looking for, and use the most appropriate algorithm for that case.

DynamicProgramming with more complex model

이상 소개된 alignment의 벌점체계는 linear score. 모든 벌점체계에 대해 일반화 하면

$$ F(i,j) = \max \left\{ \begin{array}{ll} F(i-1,j-1)+s(x_i,y_i) & \textrm{} \\ F(k,j)- \gamma (i-k) & \textrm{k=0,...,i-1} \\ F(i,k)- \gamma (j-k) & \textrm{k=0,...,j-1} \end{array} \right $$

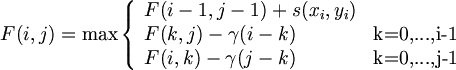
But, This procedure now require O(n^3), because in each cell (i,j) we have to look at i+j+1 potential procursors, not just three as previously. 그러나, k의 검색이 제한될 수 있는 조건하에서 O(n^2)로 계산 가능

Alignment with affine gap scores

affine gap score structure : 벌점(g) = -d-(g-1)e

Three separate situations

  • M(i,j) : best score up to (i,j) given that xi is aligned to yj
  • Ix(i,j) : xi is aligned to a gap (in an insertion with respect to y)
  • Iy(i,j) : yj is in an insertion with respect to x 

              { F(i-1, j-1) + s(xi, yi), 
F(i,j) =  MAX { Ix(i-1, j-1) + s(xi, yi),
              { Iy(i-1, j-1) + s(xi, yi);

Ix(i,j) = MAX { M(i-1, j) - d,
              { Ix(i-1, j) - e;

Iy(i,j) = MAX { M(i, j-1) - d,
              { Iy(i, j-1) - e.

This will be true for the optimal path if -d -e is less than the lowest mismatch score. It can be described FiniteStateAutomata (FSA)

Two state [FSA]로 표현하면, 

F(i,j) =  MAX { F(i-1, j-1) + s(xi, yi), 
              { I(i-1, j-1) + s(xi, yi);

              { M(i, j-1) - d,
I(i,j) =  MAX { I(i, j-1) - e,
              { M(i-1, j) - d,
              { I(i-1, j) - e.

This type of automaton can account for the two-state affine gap algorithm, using extra transitions for the deletion and insertion alternatives. linear gap cost is one-state algorithm.

Simpler state-based automata are called MooreMachines, and transition-emitting systems are called MealyMachines

More complex FSA models

DynamicProgramming algorithm의 FSA 표현의 장점은 새로운 형태의 algorithm을 만들고, 작동형태를 이해하기 쉽다는데 있다. 이 방법으로, intracellular, extracellular or transmembrane regions등의 특정한 alignment 규칙을 만들 수 있다. 1997년 Birney & Durbin에 의한 보다 복잡한 scenario를 이용할 수 있고, Searls & Murphy 는 1995년부터 FSA에 대한 보다 명확한 정의를 내리고, 이것을 만들기 위한 interactive tool을 개발해오고 있다.

BiologicalSequenceAnalysis Chap.4에 state model을 이용한 PairwiseAlignment가 소개되어 있다.

HeuristicAlgorithm

이상 언급된 sequence alignment 방법들은 충분히 빠르지 않음. 현재의 Database내의 내용과 일일이 비교하기에 너무많은 시간이 소요됨. 따라서 보다 빠른 방법이 요구됨.

The goal of these methods is to search as small a fraction as possible of the cells in the DynamicProgramming matrix, while still looking at all the high scoring alignments.

We must use heuristic approaches that scrifice some sensitivity, in that there are cases where they can miss the best scoring alignment. Two of the best-known algorithms BLAST, FASTA

BLAST

The BLAST package provieds programs for finding high scoring LocalAlignment between a query seqnence and a target database. We can look initially for such short stretches and use them as 'seeds', from which extend out in search of a good longer alignment.

BLAST makes a list of all 'neighborhood words' of a fixed length (3 for protein, 11 for nucleic acid)

FASTA

FASTA uses a multistep approach to finding local high scoring alignments, starting from exact short word matches, through maximal scoring ungapped extensions, to finally identify gapped alignments.

The first step uses a lookup table to locate all identically matching words of length ktup between the two sequences. (ktup 1, 2 for protein, 4 or 6 for DNA)

Linear space alignment

LinearSpaceAlignment

Significance of scores

How do we decide if it is a biologically meaningful alignment giving evidence for a homology?

The Bayesian approach: model comparison

Probability that the sequences are related as opposed to being unrelated --> P(M|x,y)

PrioriProbability P(M) that the sequences are related, and hance that the match model is correct. and P(R) = 1 - P(M)

PosteriorProbability P(M|x,y) that the match model is correct, and hance that the sequences are related, is 

           P(x,y|M) P(M)         P(x,y|M) P(M)              P(x,y|M) P(M) / P(x,y|R) P(R)
P(M|x,y) = ------------- = ----------------------------- = ---------------------------------
               P(x,y)      P(x,y|M) P(M) + P(x,y|R) P(R)   1 + P(x,y|M) P(M) / P(x,y|R) P(R)

Let    S' = S + log( P(M) / P(R) )

Where  S = log( P(x,y|M) / P(x,y|R) )

Then   P(M|x,y) = σ(S')

Where  σ(x) = e^x / (1 + e^x)

σ(x) is LogisticFunction.

Given a fixed prior odds ratio, the expected number of (falsely) significant observations will increase linearly.

The Classical approach: the extream value distribution

We can look at the distribution of the maximum of N match scores to independent random sequences. If the Probability of this maximum being greater than the observed best score is small, then the observation is considered significant.

Score of a match to a random sequence --> Sum of many similar random variables --> approximated by NormalDistribution.

asymptotic distribution of the maximum MN of a series of N independent normal random varibales 

P(MN <= x) =~ exp( - K N e^(λ(x-μ)) )

This form of limiting distribution is called the ExtremeValueDistribution or EVD. If this is less than some small value, such as 0.05, 0.01, then we can conclude that it is related.

Karlin & Altschul은 1990년에 EVD를 analytical하게 유도해내었다.

  • The number of unrelated matches with score greater than S is approximately PoissonDistribution.

    •  E(S) = K m n e^(-λS) 

  • where λ is the positive root of

    •  SUM(Qa Qb e^(λ s(a,b)) = 1

  • The Probability that there is a match of score greater than S is then

    •  P(x > S) = 1 - e^(-E(S)) 

It is common not to bother with calculating a Probability, but just to use a requirement that E(s) is significantly less than1. This converts into a requirement that 

        log mn
S > T + ------
          λ

Mott 1992년에 gapped alignment scores를 제안함.

Correcting for length

Database내의 little related long sequence가 high related short sequence보다 높은 점수를 받는 경향이 있다.

A theoretically justifiable correction for length dependence is that we should adjust the best score for each database entry by subtracting log(mi).

Why use the alignment score as the test statistic?

This would seem to prevent the problem that the search phase increases the background level when testing. However, we need both the search and significance thest to have as much discriminative power as possible.

Deriving score parameters from alignment data

How to determine the components of the scoring model, the SubstitutionMatrix and gap scores.

It should be clear that the performance of our whole alignment system will depend on the values of these parameters, so considerable care has gone into their estimation.

Simple approach

  • count the frequencies of aligned residue pairs and of gaps in confirmed alignments
  • set probabilities Pab, Qa, and f(g) to the normalised frequencies.

Two difficulties with simple approach

  1. obtaining a good random sample of confirmed alignments
  2. different pairs of sequences have diverged by different amounts.

This suggests that we should use scores that are matched to the expected divergence of the sequences we wish to compare.

Dayhoff PAM matrices and BLOSUM matrices

SubstitutionMatrix

Estimating gap penalties

time-dependant gap model은 time이 증가하면서 linear하게 벌점이 증가하므로, 적절치 못하다. 따라서,

Affine gap model에서는

  • gap-open score d linear in log t,
  • gap-extend score e would remain constant.

Gonnet, Cohen & Benner는 1992년 실험적 데이타로 부터 새로운 모델제시

  • 벌점(g) = A + B log t + C log g

We should include in our SubstitutionMatrix score a term for the probability that a gap has not opened. 

P(no gap) = 1 - 2 SUM(f(i))

SubstitutionMatrix score has to correspond to a match 

s'(a,b) = s(a,b) + log P(no gap)

PairwiseAlignment using HMMs

PairHmm

PairwiseAlignment (last edited 2013-08-25 11:41:48 by 221)

web biohackers.net